おことわり
前回の『四字熟語』まみれの記事の続きの側面もありますが、
今回のお話は、『ガチガチの!?』数学のお話です。
普段の私の独特の表現も加味されて、余計に濃い味となっております。
1000人いて、999人は理解できないと考えております。
しかし…
そもそも
こうして、物を描くという事は、実は、たった1人の、その人に向けて物を描き遺している
という側面もあります。
私が、これまでにしていることです。非効率であり、また、何の対価も、ぼぼ得られない。
どちらかと言えば、人を傷つけたり、人を怒らせたり、人をイラつかせたり、
…
それでも、たった1人の、その人に向けて物を描き遺す行為は、
確かに、其処に『景色』がある。
という事実の照明(明るく照らし、しかも、証明でもある。)にもなります。
なので、私は、とにかく物を描くことを続けております。
なので、今回も、いつもどおりで、このまま、お話を続けます。
与えられた2つの数 a と b の『相加平均』と『相乗平均』は…
以下の、描いてある『絵』の意味が、解る人…どれぐらい、いる(存在している)のかな…
『絵』は、僕が描きました。
時、場所、その瞬間に、あるいは、時代を超えて、其処に横たわる
『景色』
が、至る所にありますが、その1つです。
あなたが、ドライブや旅行で、出かけた先で、いい景色だと、あなたが、感じたものを、
あなたが、持参したデジカメで撮る。
僕がしていることは、それと同じことです。
(僕、個人的には、そのつもりなんですが…)

『相加平均』と『相乗平均』とは…!?
前回のお話で、やたらと『四字熟語』が絡んでしまいましたが、その流れにも似ています。
『相加平均』と『相乗平均』
…
これから(今回は)、数学のお話なのだけれども…例えば…数学を理解をするにしても、
あるいは、ひとつひとつの『言葉』を
理解するにしても、そのプロセスは似ていると、僕は今回、改めて感じました。
また…理解するに至るには、ある種の特別な『感覚』が必要になるのかもしれないと、僕は感じました。
ある種の特別な『感覚』?
例えば…以下の、数学の問題などで、その、ある種の特別な『感覚』が、あなたに伝わるのかもしれない。


上記、問、問題の答えを僕が、ここに記すことはしません。
僕が、あなたに求めることは、というか求めるとしたら、
上記問題の答えが解った上で、
その貴方の思考のプロセスを観察してほしい。(これを『観心(かんじん)』といったりします。)
そのときに、先に、僕が言った
『また…理解するに至るには、ある種の特別な『感覚』が必要になるのかもしれないと、僕は感じました。』
その意味が解るのかも知れません。そして、さらに、今、改めて僕が、感じていることですが、
…理解するに至る、ある種の特別な『感覚』は…
誰もが、獲得できるという保証は何も無く…いや…どちらかと言えば、獲得出来ない事の方が大多数なのでしょう。
さらに、もしあなたがこの感覚を獲得しようとし、その獲得するためのプロセスにおいて、それぞれの個人に
物凄い才能の差を感じたりするのかもしれません。
寒々しく、そして、悲しい現実が此処にあります。
…理解するに至る、ある種の特別な『感覚』は…獲得出来ないのか…
ただ、此処に希望もあります。先人たちは確かに言葉で、その希望を遺してもいます。
『継続は力也!!!』
『石の上にも三年(石の上にも三年いれば暖まる)』
『桃栗三年柿八年』
それから…
『論湿寒貧』
…
キリがないので、このあたりで、お話を先に進めます。
既に、気付いていらっしゃる方も、いるかもしれませんが…
僕の描く記事は、常に、
…理解するに至る、ある種の特別な『感覚』…
これが必要です。今回は(今回のお話では)、より必要になります。
与えられた2つの数 a と b の『相加平均』と『相乗平均』は…
以下、与えられた2つの数 a と b の『相加平均』と『相乗平均』を考えます。
認識できる数という事で、辺の長さとして認識できるという事で、実数で0より大きい。数と致します。
今回のお話の冒頭の写真で、出来上がっている物を、先ず、お見せいたしました。
ああ…先に、僕の独り言です。
出来上がっている物を見て、あるいは、見えて観えたつもりになるのか…理解できたつもりになるのか…
何処から来て、何処に、辿り着き、そして、何処へ向かおうとしているのか…
僕の場合の(今回の)出発点は、以下からです。
(問題)与えられた2つの数 a と b を基にして、その『相加平均』と『相乗平均』を
1つの絵の中に、収めることは出来ないのか?

これを、出発点として、此処から、『作図(数学の作法のひとつ)』という技術で、先へ進みました。
そして、出発点から進んで辿り着いた先で、見える景色が、冒頭でも紹介した景色にります。

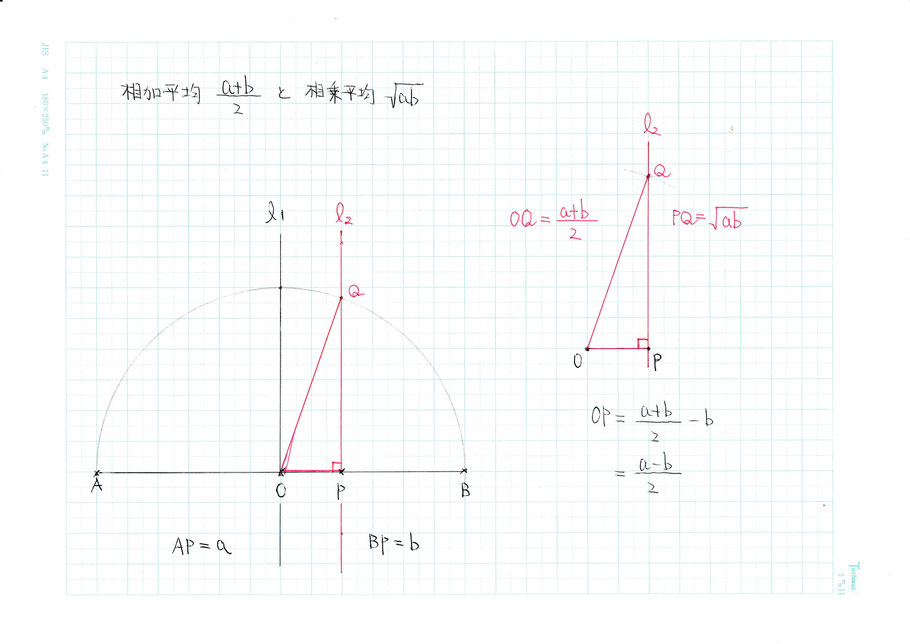
僕は山岳ガイドではありませんが、山岳ガイド風に、この出来上がった『絵(景色)』の説明をすると、
最初に与えられた2つの数、a、b、を基にして、
其処から、作図(という作法)を用いて、
その2つの数、a、b、の『相加平均』と『相乗平均』が、
円や直角三角形という特別な図形と、相伴って出現する。
という事です。さらに補足を与えるのなら
2つの数、a、b、の『相加平均』は、本質的には、垂直二等分線の作図により得られます。
2つの数、a、b、の『相乗平均』は、先に得られた『相加平均』を半径とする円を考えることと、
巧い位置で直角三角形を考えて、其処で、三平方の定理を用いると得られます。
『相加平均』と『相乗平均』を得ようという操作を繰り返すと…
今、2つの数、a、b、の『相加平均』と『相乗平均』が、得られました。なので、この、得られた
『相加平均』と『相乗平均』を基にして(これを2つの数、a、b、だと思って、)、
これの、『相加平均』と『相乗平均』を得ることが出来ます。実際にやって魅せると…

絵からも解る通り、限りなく
『相加平均』 ≒ 『相乗平均』
となる。と成ってくることがわかります。潰れている直角三角形を目の当たりにします。
さらに、このような同じ操作を幾度となく繰り返し続けると、…
これは、何をしているのかというと、
『相加平均』によって、作られていく数列と、
『相乗平均』によって、作られていく数列と、
2つの数列を目で見ることが出来ます。
それぞれの数列の極限値が、(極限値として)
『相加平均の数列の極限値』=『相乗平均の数列の極限値』
となることが、知られています。この事実を『算術幾何平均』と呼び、
最初に与えた2つの数、a、b、に対する、その『算術幾何平均』を
(『相加平均』や『相乗平均』によって作られる数列の極限値を)
AGM( a, b )
数学において、以上のように表記します。(このように表記したりします。)
補足:数学において算術幾何平均(さんじゅつきかへいきん)を、
英語では:Arithmetic-geometric mean と表記します。
これらの単語の、その頭文字をとって表記しています。
今回のお話で、辿ってきた『道』をおさらい…
(問題)与えられた2つの数 a と b を基にして、その『相加平均』と『相乗平均』を
1つの絵の中に、収めることは出来ないのか?

そして…その答えが…
1つの問題の答えを通じて、
円、直角三角形、相加平均と相乗平均、これらが結びついている景色を観て
さらに
この操作を…もう1回繰り返す…それだけで…
潰れていく直角三角形を目の当たりにし
…

このような操作を幾度となく繰り返した先で、以下のような『観心』を行う。
出発地 ⇒ 辿り着いた地
この上記の矢印の意味とは?
『道』?
『景色(道から、観た)』?
すると
…
本来は、此処に、これより先のお話を続けるのなら
算術幾何平均、楕円積分、そして、超幾何関数、などの事も記さなければ、ならないのだろう。
それから、lemniscate曲線のこと。Gaussの事も。実際にGaussは
AGM( 1, √2 )
を計算している。其処で、不思議な景色を観ることが出来るのだが、
これより先は、その詳細は、かつての僕のように数学という道を歩む覚悟のあるものに委ねることにしよう。
1つの一個人のブログ記事の中に、これらのお話まで、僕が描くのは、控える。
ただ、これらは、既に知られていることで、数学科の大学生4年生ぐらいから、数学専攻の大学院生が読むような、
数学の専門書として、何冊もの本が出版されている。僕からは、取り敢えず、以下の1冊だけ紹介しておく。
著者:梅村 浩
タイトル:楕円関数論(楕円曲線の解析学)
出版:東京大学出版会
この本の第6章に、算術幾何平均と楕円積分の関係が丁寧に描いてある。そして、Gaussが観ていた
AGM( 1, √2 )
という、不思議な景色も、この本の第6章に描いてある。
尚、今回のお話の締め括りに、これから、僕個人の場合の応用(援用)を紹介する。
そして、問題を『あなたの場合』に書き換えて、その『あなたの問題』を解くというのであれば、
上記に挙げた本を皮切りに、さらに、何冊もの関連する数学の専門書を読み込む必要が出てくることになる。
まあ…僕自身がそうなのだが、実際には数学の専門書だけでは済まないのだが…
今回のお話の応用(援用)
以下、より、此処からのお話は、殆どの人に理解されないのだろう…
此処で、これから披露するものは、僕自身の『観心』という行為になる。
そして、さらに、もし、その意味が解る、理解する者(人)が現れた時に…
それが、善用されるとは限らない可能性もある。
(僕らは、既に少なくともプーチンという人間を見ている。安倍晋三という人間を見ている。)
まあ…どんなことを『する』しても…必ず『リスク』は存在する。
なので、
いづれは、僕よりも、才能のあるものが出現し、そのものが、善用することを期待して、
僕は、今、改めて、いつものように1歩を刻む。
takumaroは今日も往く!(2023.02.07、記)
以下、提示している問題は、極めて、僕の個人的な問題の記述をしている。
もし、この問題を解くのなら、
それは、『あなたの場合』として、問題を書き換えて、挑戦してほしい。
(僕の場合)
最初に与えられた2つの数に相当するもの:数学と柔道
相加平均と相乗平均に相当するもの:これも…多分、数学と柔道…実際には、此処に、さらに修験道や仏教も絡んでいて…
相加平均と相乗平均に相当する行為を、繰り返した先では? 取り敢えず、僕の場合は、これらを以下のように表記
AGM(数学、柔道)
(僕の場合に浮上した問題、残念ながら未解決)
問題1,特別な図形、円や直角三角形、lemniscate、派生し現れる円周率 π …
以上のような不変的な具体的な値、特別な図形として目で見えるものは、これらに相当するものは存在するのか?
問題2,繰り返されていくプロセスの中に、超幾何関数のような、網羅してしまうものが、存在するのか?
(僕の予想)
問題1,問題2,に関する答えは、全ての人に見いだされるもの。援用しやすいもの…


















