三平方の定理…の証明！？（その１）（第４話）

年も明け、大夫時間が経ってしまった。僕にとっては、毎年恒例の感覚になる。

未だに、年賀状の返事も描いていない。返事を出すつもりではいるのだが。

（年賀状の返事を出すつもりだが、『返事を出す！』…と断言できない自分が悲しい…）

『継承』

という事を意識して、数学の直角三角形に関する三平方の定理（または、ピタゴラスの定理）の

ことについて、ずっと、去年の１２月頃ぐらいから考えていた。勉強をしていた。

ある程度、纏まった世界が個人的には体感できたけれども、さすがに、全部は此処では出来ないのだろう。

今回のを含めて、３回、

三平方の定理（別名：ピタゴラスの定理）の証明

という内容でお話をしたいと思う。

僕がしているのは、お話であり、物語を描いている。

だから、時々、物凄く角が立つ表現が在ったりする。

でも、その角が立つ表現の中に意外と本質が在るのだと、僕は思うし、また、そう感じている。

いつも間にか、クリスマスも、大晦日も正月も過ぎ去っている。

確かに、１年中、何らかのイベントが在るのかもしれないが、

僕からすると、ただ、連続的な日常が積み重なっている。

それだけである。

新年の挨拶はさておき、早速本題に入ろう。

数学的な事実を、また別の観方を与えて（本質的な意味を変えずに）、証明をする。説明をする。

直角三角形とそれぞれの辺の長さをもつ正方形たち、とそれらの面積の関係を考える。

こういう、以下の赤い線が引けるか！？という難問は在るのだが…

（こういう事に、気付けるか？という事）

此処で、使っている技術は等積変形という物になります。

（２つの三角形が合同でなくても『底辺』と『高さ』が同じだったら、２つの三角形の面積は同じ。）

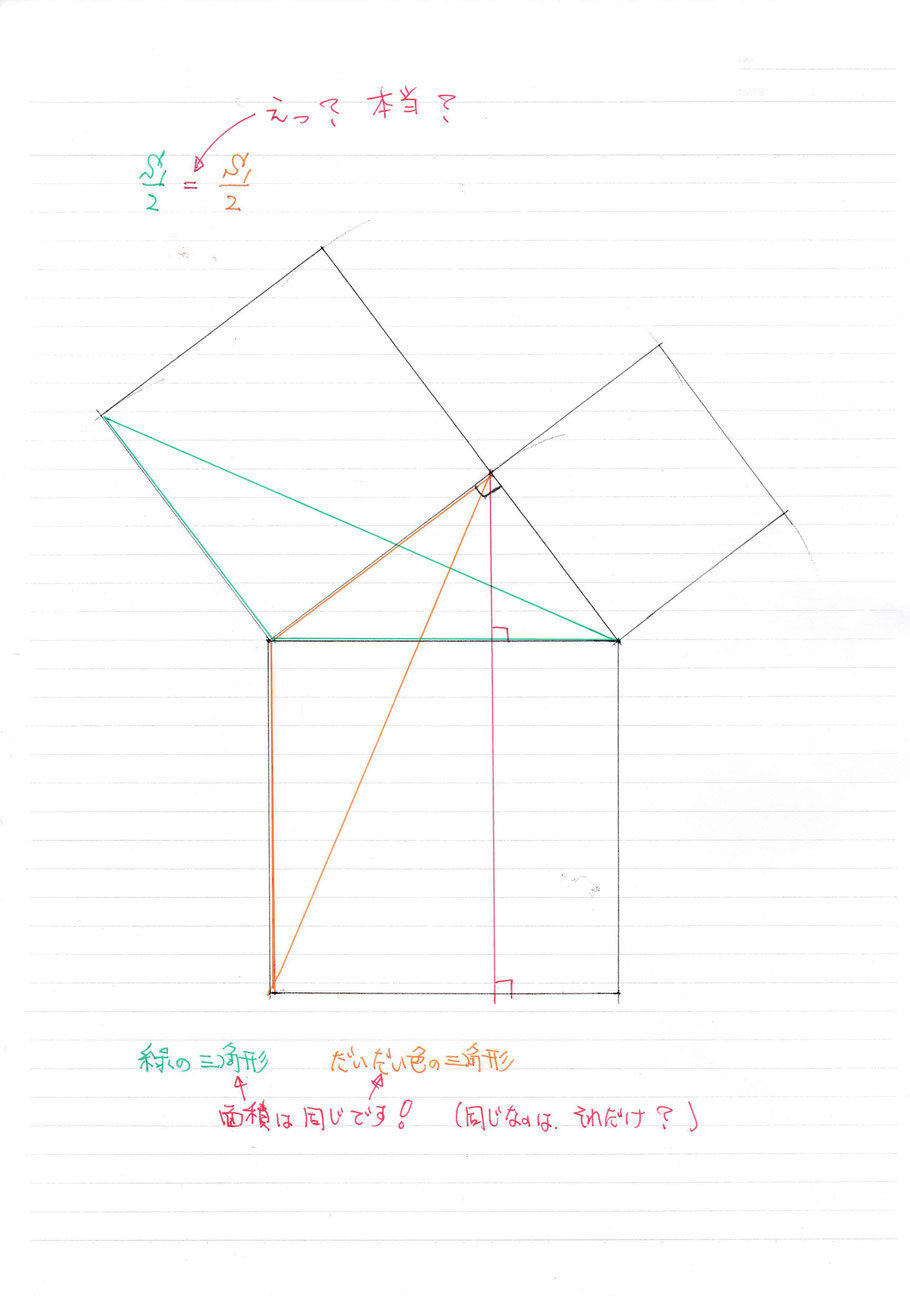
以下の、図が、この証明の１つの『肝』なのでしょうか…

以下の図の緑色と橙色の２つの三角形の面積は同じです。

何故なら、この２つの三角形は『合同』だから…

では、

「その、２つの三角形の合同と主張できる、合同条件は？」

図から、解ります。考えて見ましょう。

（ヒント）僕は、最初にこの話を人から聴いたときに、９０度頭を回転させて図を眺めていました。

以下は、最初に説明した『等積変形』と同じです。

此処までの議論を繋げ合わせると…

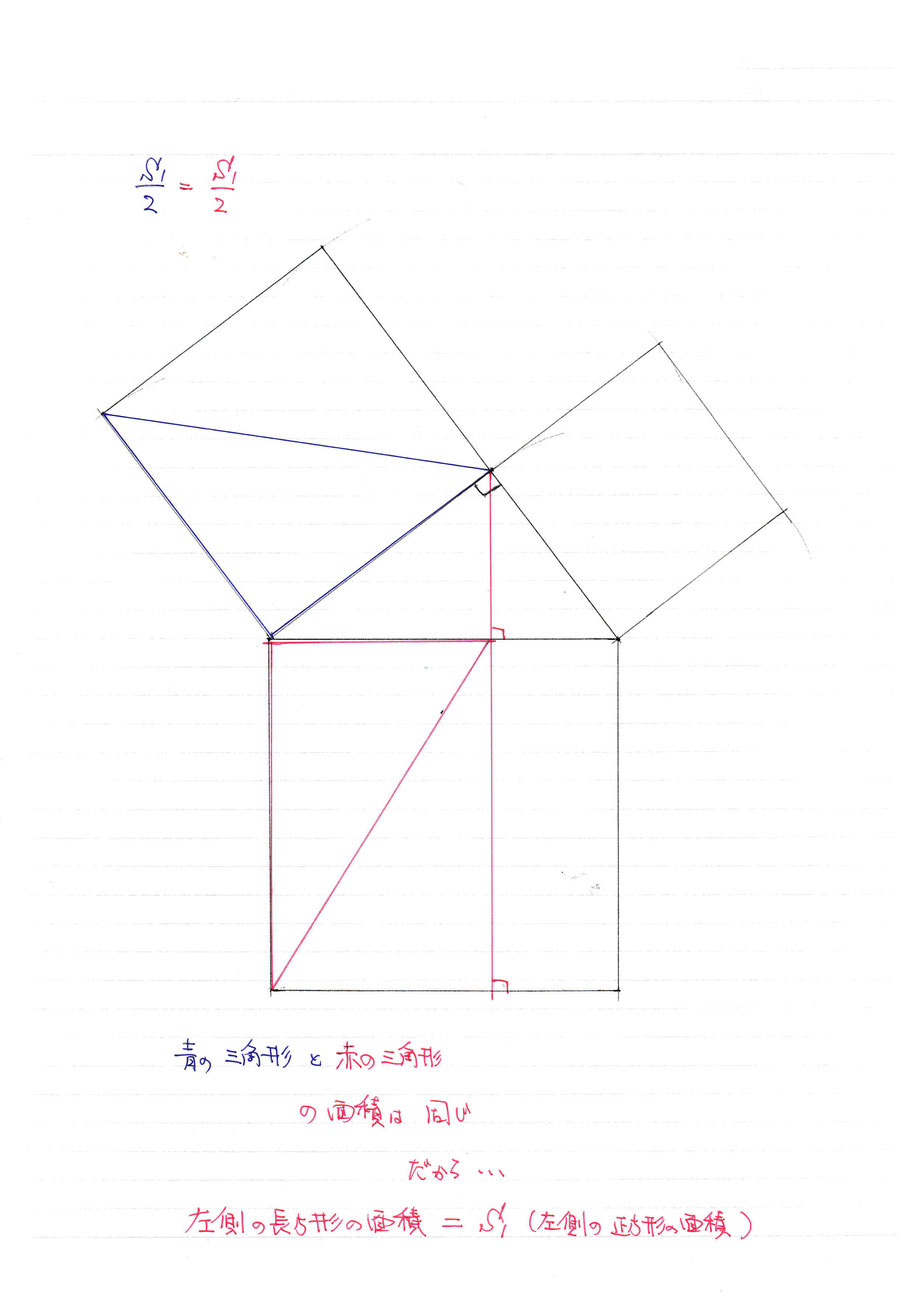
此処までで、何が解ったのか？改めて書くと

左側の正方形の面積と、赤の線で仕切られて出来た、下の正方形の左側に出来た長方形の面積が同じ！

という事が解りました。

随分と、数学者特有の、数学特有の乱暴な所作かも知れませんが、

『同様にして』

…

右側の正方形の面積と、赤の線で仕切られて出来た、下の正方形の右側に出来た長方形の面積が同じ！

という事が得られます。それで、証明が出来上がります。

それぞれの証明に於いて、『肝』が在ります。今回は…

１、互いに合同でなくても、底辺と高さが同じ２つの三角形は、面積が同じ。

２、図から、合同な２つの三角形が出現する。（合同条件は、３択なので、各自で気付いて下さい。）

の２つでしょうか…まあ…最初に図から（気付いて）、赤の線が引けるか？という難問が在りますが。

通常、こういう、思考の流れを、１枚の図の中に、全て書き込むのだろうか…

この証明は、僕は大学の教職課程（数学の教員免許を取得するための課程）で習ったが、

その時は、その講義の中では、１枚の図の中に、全てを書き込んでいた。

今回、僕としては、思考の流れを辿って欲しいから、１つ１つの思考に対して、同じ図を何度も用意した。

複数のページに分けた。

それから、数学者特有の、数学特有の乱暴な所作…

『同様に』とか『自明である。』

僕は、今回、図の左側に対してした操作（あるいは技術、思考を）を、図の右側に対して同じようにするだけなのだが…

やはり、感じ方には差はあるのだろう。これは、数学のお話である。例えば…

「右腕でボールを投げれるの？じゃあ、左腕でボール投げれる？」

とか…

「クロールが得意なんだ…背泳ぎも得意！？」

とか…

僕は、柔道の稽古を続けているけれども

「右組で出来る事…左組でも出来る事…」

と言った具合にである。

ちなみに、基本柔道では本音は、誰もが、殆どの人が（少数の例外はあるが…）、

右組、または、左組の、利き組がある。けれども、建前では、柔道では

『右組でも出来る事を、左組でも出来るように成りなさい。』

という事を平然と求めて来る。初段昇段のために、また、最初に習うであろう柔道の形の『投の形』が、

１つ１つの技に対して、右組で技を極める事。左組で技を極める事。その両方を求めている。

『総体柔らかく…』は数学や柔道と言ったものに限定した話でもないのだろう。

『総体柔らかく…』中々、ハードルは高いのだが…

『総体柔らかく…』野球だと『走攻守』とでも言うのだろうか…

『総体柔らかく…』と言うわけでは、ないが、『数学の三平方の定理の証明』と、かなり限定しても、その幾つかを

紹介したいと思う。（勿論、それぞれに、証明の肝は異なる。）

『総体柔らかく…』を１つの目標に…先ずは、僕の場合、頭を柔らかくすることからかな…

takumaroは今日も往く！