長い年月を経て、この『景色』が在るのだが…

確かに、長い年月を経て、この『景色』が在る。
気の遠くなるような、時間の経過が其処には在る。
そういう物だと思って、あるいは、そういう事だと感じて
『景色』
を観ている人はいるのだろうか…
(写真の場所は、鳥獣保護区になっている。悠久の時を感じる事の出来る場所で、心と身体を休ませていた。)
そもそも、物、事、が、『熟成されるまで』『出来るようになるまで』『解るようになるまで』、
『観る事が出来るようになるまで』には、
相応の時間が必要になる。植物が育って行くことと同じである。
『桃栗三年柿八年…』
これが、大自然の摂理である。改めて
『桃栗三年柿八年…』
では
『人は…?』
数学者、岡潔が、『わかる(解る)』という事について、段階的に分けた話をしている。
これを、少し、僕なりに感じる処があり、6段階目を付け足し整理したものを以下に再び紹介する。
参照参考:「日本のこころ(講談社文庫)」昭和49年7刷り p183--184
『わかる(解る)』
1段階:感覚的にわかる
2段階:形式的にわかる
3段階:意味がわかる。理解する。
4段階:意義がわかる。
5段階:体取する。体得する。
6段階:体現する。体現者になる。
これだけを見ても、相応の時間が掛かると僕は感じてしまうのだけれども…
数学にしても、柔道にしても…である。尚、大抵は、上記のような順で、心の働き、それから、身体の働き、が
順に起きて行くのだが、中には、例外もある。例えば
子供なんかは、時に、いきなり教えた内容を体現をしたりする。
「人が、何年も掛かって獲た感覚を、彼らに話すと、彼らは一瞬で感覚的な理解をし、さらには、体現をしたりする。」
…
以下は、僕の場合のお話。
例えば…柔道の場合、
僕は、形の中に在るある一つの技の中の、受けの動作が出来るようになるまでに…形の稽古を積みつつ結局、
『8か月』
という時間を要した。
また、形の稽古を積みつつ、そこから『何か』を感じられるようになるまでには、
少なくとも
『1年』
という時間が要るようだ。
数学では、感覚的に気付いた数学の個人的な発見と、その価値を世間に認めさせるまでに(論文雑誌に載るまでに)
10年を要した。
「まあ…いずれも僕が、他人以上に不器用である…という事も在るのかもしれないのだが…」
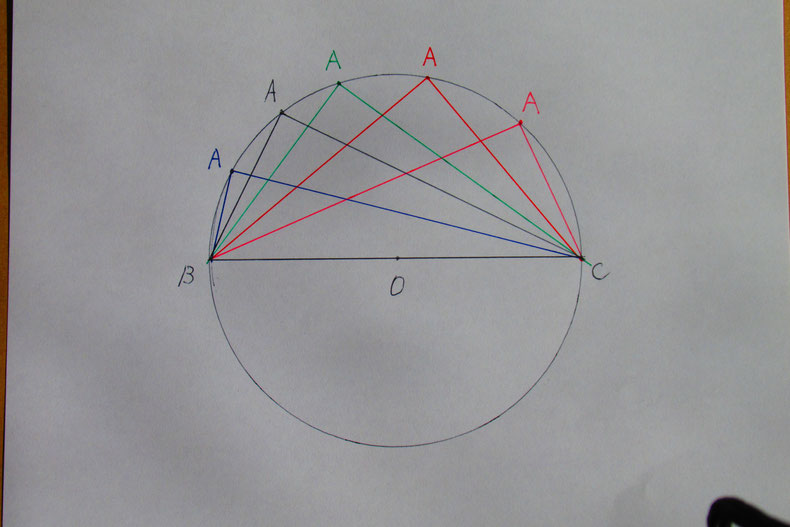
今回の一連の円周角のお話にしてもである。
考え方の真似をする。結果から考えてみる。特殊な場合を考えてみる。そういう観方に慣れる…
画が映し出している景色…でもその景色が観えるように成るのには時間が掛かる。
石の上にも三年…籠山12年…
これまた、僕の場合のお話。個人的な経験に基づくお話。
3年…その事を意識して続ける事が出来れば(これが、難しいのかもしれないが)、それなりに景色が観えて来る。
10年…その事を意識して続ける事が出来れば(これが、更に難しいのかもしれないが)、それなりの『高み』と其処からの
応じた景色が観えて来る。
でも、大半の人は、『その事を』意識して続ける事が出来ないし、だから、
『高み』に立つことも、そして、其処からの景色を観る事もない
…
また、逆に
…
『その事を』意識して続けて
『高み』に立ち、其処からの景色が観えたとしても…
共感出来る者が現れるのは、未来のお話…という事だってありうる…
そもそも、『その事だけ』が出来るわけでもないのだから…
生きて往けば、どうしたって、煩わしい事や、誰もが直面する事に向き合わされる事もある。
観念的な言い訳だが、こうしたブログですら描けないときもある。だから
悠久の時を感じる事の出来る場所で、心と身体を休ませていた。
…
『解ること』『観えること』

『わかる(解る)』
1段階:感覚的にわかる
2段階:形式的にわかる
3段階:意味がわかる。理解する。
4段階:意義がわかる。
5段階:体取する。体得する。
6段階:体現する。体現者になる。
これに、更に加えると、『知識』や『経験』が必要不可欠なのだと思う。『知識』が在れば、また、『経験』が在れば、
(例えば)上のメモから、これから、僕がどんなお話を考えているのかが解る。
知識としての『三平方の定理(ピタゴラスの定理)』
それから、
経験として、三平方の定理を満たす数を探したこと
これらが、在れば…である。
『三平方の定理(ピタゴラスの定理)』とは、直角三角形に関係する数学の定理なのだが、
確かに、直角三角形は特別な三角形だ。でも、その直角三角形だって、無数に考える事が出来る。
「確かに、直角三角形は特別な三角形だ。でも、その直角三角形だって、無数に考える事が出来る。
その事を、今までの知識と繋がるような、景色として魅せるには…」
「…何を書いていたのですか…?」
「ああ…最近は、直角三角形の事について、考えているんです!聴いてくれます?」
少しの間の後に、苦笑い交じりで
「朝から、そんな暗い話…もっとファンキーな話のネタを用意して下さい。」
「えっつ…でも…○○さんは、聴いてくれましたよ!」
「否!私は結構です。」
少しの間の後に
「そうですよね…僕のお話(特に数学のお話)は、始めた途端に、『否!もう無理です!』と拒絶される事が
殆どですからね…それは、それで健全な反応だと理解はしていますが…」
「理解は、されているんですね…でも…本当は、○○さんだって、無理して、我慢して聴いているんじゃないですかね…」
「え~っつ!!」
「ほら、私のように、はっきりと『否!』とか、自分の意志を示すのって大変な事ですからね…」
「…」
「かわいそうに…私のように、はっきりと『否!』って言えば、楽になるのにな…○○さんも!」
「え~っつ!!」
あなたも、実は我慢して僕のお話を聴いている事に感謝しつつ
takumaroは今日も往く!
『景色(無数の直角三角形)』