今、僕らが観ている景色は…(場合①)

僕らは、殆どの場合、出来上がった物を見せられる。(…事の方が多い。)
知識が在れば、上の図だけで、僕が何の話をしているのか解る人もいると思う。
そう、ずっと円周角の定理のお話を続けている。
今回、僕が言いたいことは、
『分岐した世界の果て…でも…』
になる。何処に『視点を(焦点)』合わせるか…その事に依って、意味する物も違って来る。
今回のお話の意味する処は、円周角の定理のそれぞれの場合でもという話。
円周角の定理とは、円周角と中心角の特別な関係の事をさす。
(それぞれの場合を考える必要があるが、その中の1つの場合が上記になる。)
(円周角の定理とは…)
中心角 = 2 × その円周角
上記場合①だと
∠BOC = 2 × ∠BAC
他にも様々な場合に、このような関係式が成り立つ
追記:新しい事(知らない事、未知の事、…)を学ぶという事は、同時に、様々な言葉の意味を確認する事も求められる。
(言葉の確認)
弦:円周上の異なる2点を線分で結んだもの(上図の弦BCのこと)
円周角:円周上の異なる2点(弦の端点)と、円周上のまた別の点とで、出来る∠のこと。(上図の∠BACのこと)
中心角:円周上の異なる2点と、円の中心Oとで、出来る∠のこと。(上図の∠BOCのこと)
(場合①に於ける証明)
上図の、緑の線は補助線になる。証明を与える目的のために、適切な補助線を引く事になる。(これが出来ないと嵌る…)
点Oは、円の中心なので、⊿OABと⊿OACは、共に、二等辺三角形になる。
三角形の
1、3つの内角の和は180°である。(外角の1つは、2つの内角の和になる。)こと
2、二等辺三角形の2つの底角は 、互いに等しい。
以上の性質を使う。
適切な補助線を引くのは、上記1、2の、性質を用い易くするために、である。
∠OAB=αと置くと、⊿OABは二等辺三角形なので、∠OBA=αとなり、よって、この2角の和、
外角の1つ∠BOD=2α とかける。
同様に、(『同様に』:(意味)数学では、同じような論理展開をまた別の『処』で扱ったりする。よくあることである。)
∠OAC=βと置くと、⊿OACは二等辺三角形なので、∠OCA=βとなり、よって、この2角の和、
外角の1つ∠COD=2β とかける。
此処までのお話をそれぞれにおいて場合①の図を元に整理する。
中心角 ∠BOC = ∠BOD + ∠COD = 2α + 2β = 2(α + β)=2 × 円周角∠BAC
円周角 ∠BAC = α + β
場合①の証明は、これで終わる。
分岐した世界の果ての、それぞれの『画』…それでも尚…
『円周上の点Aをどのような位置に取るのか…?』
この選択で、見る事の出来る『画』が変る。
それから…そもそも…
『どのような『弦』に対して、円周上の点Aを取るのか…?』
いずれにしても、円周角の定理は成立する。ちなみに、
円Oの半径は、皆同じである。4cmで僕は描いた。また、弦BCも同じに描いた。6cmにして描いた(…と思う。)。
つまり、場合①、場合②、場合③に於ける、中心角は、皆同じだから、何故なら、
中心角∠BOCを構成する、⊿BOCが合同だから。此処までは、当たり前のお話、だけども…これを受けて
『場合①、場合②、場合③、と見た目が異なるそれぞれの場合の円周角∠BACは、皆、互いに等しくなる。』
場合②(点Oが⊿ABCの辺上に在る)

場合③(点Oが⊿ABCの外側に在る)

場合④(点Aを弦BCの反対側に取ると…)
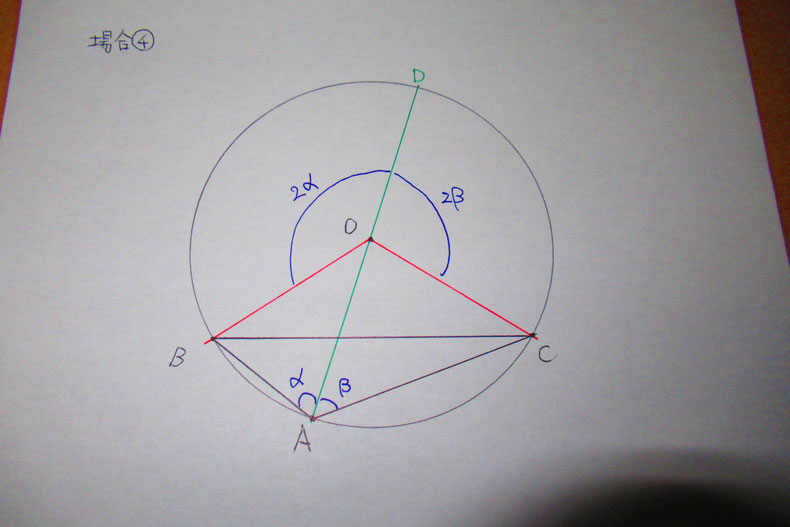
場合④は、点Aの取る位置を、弦BCに対して、今までとは『反対側に』取っている。
なので、中心角や円周角の場所が、今までのと『反対側に』なる。
だけども、基本となる考え方は同じなので…
これこそ、『数学のマジック!?か』…
意味を知りたければ…
場合①は証明を与えたから…場合①の証明を観ながら、場合④の『画』を観る事を僕は勧める。
場合⑤(弦が『特別な』場合)

円周上で異なる2点を取り、それを線分で結んで『弦』を考える。つぎの2つの場合しかない。
1、『弦』が円の直径になる。(特別な場合。)
2、『弦』は円の直径とはならない。
特別な場合なので、この時は、円周角、中心角、共に具体的な角度が解る。
今のところ、『円周角の定理』のお話を続けています。理由は…
(再掲)
いずれ、『本』として、纏めるので、僕から搾取するのではなく、僕の事を然るべき待遇で迎える事の出来る
出版社の方は、僕に打診を下さい。
また、念のために…
記事の閲覧は結構ですが、私の著作権を侵害する行為はなさらないようにお願い申し上げます。
何処から観るか…何処にいるのか…その景色は随分と異なる。
僕は、長く『数学』も続けて来た身の者です。その僕が、こうして
具体的な景色を提示し続けている
という事をしています。
あと2回(次回、そして、その次)は…円周角の定理に関係するお話をする予定です。
しかし…
今回のお話では、
こうも景色の見た目は変わったのに(場合①、場合②、場合③、場合④、場合⑤)…
その本質は全く変わらない。
不思議な世界が存在する。
お話の『著者』として、現在感じている事です。いずれの場合にも、
(円周角の定理)
中心角 = 2 × その円周角
具体的には
∠BOC = 2 × ∠BAC
いずれにしても、このような関係式が成り立つ
多くの場合、僕らは出来上がった物を見せられるし、また、基本、『現在の』『その者(物)』を見る事になります。
そのような中で、改めて、其処までのプロセスや、ちょっとした工夫に着眼をすることは、大事な事です。
どこまで、既知の知識と結びつけて考える事が出来るのか…
どのような、様々な場合が考えられるのか…
どこが、分岐点となるのか…
などなど…
今回のお話は、分岐した世界の果てで、のお話です。
にも拘らず、その本質は全く変わらない。
不思議な世界が存在する。
これらは、一連の動作や、流れ、プロセスが解っていて、さらに、
思考を積み上げて感知される景色になります。
哀しきかな、哀しきかな
誰もが観る事がない景色を披露しつつ
また
誰もが解るわけでもない景色を披露しつつ
…
共感をしたいから?
遺して置く事に依る100年後の奇跡に期待して?
…
takumaroは今日も往く!
(2020.10.21、記)
あと2回の『円周角の定理』のお話の内容は…
jimdoには、描いたブログ記事を丸々コピー(複製)してくれる機能があり、その機能を使い、今回も記事を描きました。
しかし本当に…よくよく考えると、この『コピー』も、あらゆる意味に於いて、また、色んな意味に於いて、必要な技術なのでしょうか…数学に於ける『同様に』…論理展開(考え方)のコピー…そのような意味に於いても、今回のお話の中で、僕は指摘しましたが、不思議な物に気付いた人もいるのでしょうか…
しばらくの間ブログを更新できませんでした。理由は、円周角の定理のお話に決着が付いたら、改めてしたいと思っています。
それは、ちなみに言い訳というよりは、それも『一つのお話』です。
さて、僕の円周角の定理についてのお話は、後2回する予定です。内容は
『緑の補助線を引くことについて』理解を得るために、今回のお話の、場合③と場合⑤に於ける
緑の補助線を引く前の物を紹介しました。他人の理解を得るために、また、少なくとも自分が巧く現象の理解をするためにも、自力で緑の補助線を引く必要があります。
これらに加えて、以下のブログ記事タイトルの景色をまた披露したいと考えています。
ブログ記事のタイトルは…
次回:『特殊な場合の景色』
その次『コール&レスポンス』
場合③と場合⑤は、緑の補助線も含めて、場合①のような詳細な証明を付ける予定です。
場合②は、補助線を引かなくても解る場合ですよね…
場合④は、補助線を引いて、『同様に』の論理展開をして…あれ?場合①と全く同じ…!?
なので、これら場合②、場合④ついては、今回の『画』でおしまいにします。
「え?」
時に細部を自力で埋めるのも(細部を自力で観る事も)、また、鍛錬だと、お考え下さい。
では、また次回、此処に発表する記事(お話)にて、お会いしましょう。
